学術研究においては様々な要素が求められますが、その中で最も重要な要素の一つが「客観性」であり、その根幹をなすのが「データ」です。もちろん、データは集めて終わりではなく、手元にあるデータを解釈し、効果的に提示する必要があります。
「データ分析」や「データの可視化」はデータを解釈し、示す上で「客観性」を担保する強力なツールです。その一方で分析方法などは非常に多岐に渡り、適切に取捨選択するにはある程度の知識が求められます。
先行研究や所属の研究室で慣例的に行われている分析の流れに沿って、自身のデータを処理するのも一つの方法ですが、「手元のデータの性質」と「分析方法の特徴」を正しく理解すれば解釈に深みが出るとともに、分析の応用の幅も大きく広がります。
本セミナーでは統計学の基礎からパラメトリック検定、ノンパラメトリック検定、多変量解析、共分散構造分析まで、心理統計に必要なデータ分析についてRを使用しながら丁寧に解説します。
事例などで使用するデータは主に心理系データを用います、分析手法そのものは特に限定していませんので、多くの研究分野で十分応用可能な内容です。
研究者、分析担当者
統計学の基礎を固めたい方
統計的検定・各種分析方法のしくみを理解し、適確に応用したい方
(特に高度な数学の知識は必要ありません。)
220,000円(税込)
・特徴
〇統計分析ツール「R」を使用
- 統計分析に用いられるフリーソフトウェア「R」を使用します。 基礎から丁寧に解説しますので、Rを使用するのが初めてでも問題ありません。
- Rは学術団体からの信頼性も高く、論文投稿や学会発表によく用いられます。
〇統計学の基礎から学習
- 本講座では、平均や分散など基本から改めて解説します。
分散の計算ではなぜ二乗するのか、不偏分散の分母はなぜ「n-1」で計算するのか?といった内容を1つずつ丁寧に読み解くことで理解を深めます。
〇検定は幅広く学習
- 論文などで結果を示す上で「有意性」を呈示することは重要ですが、その前に「どの検定を使用するべきか?」はもっと大切なポイントです。
本講座ではt検定や分散分析などのパラメトリック検定はもちろん、ノンパラメトリック検定やその多重比較についてもご紹介します。
〇有意性と効果量・検定力・サンプルサイズ
- 結果の有意性は違いを示す上で重要な一方で、サンプルサイズ(データの数)を多くすれば有意な結果を得やすいという事実があります。
そのような背景をうけて近年では有意確率だけでなく、効果量の提示が求められることが少なくありません。
本セミナーでは効果量に加えて関連の深い検定力、適切なサンプルサイズの設定方法なども解説します。
これらの考え方自体は新しいものではありませんが、広く注目されるようになったのは比較的最近のことです。
〇多くの分析方法をご紹介
- 回帰分析、主成分分析、因子分析などの出現頻度の高い分析方法についてそれぞれの細かな手法の設定を含めた解説、及びそれぞれの分析方法の使用方法に加えて、複数の分析を組み合わせた分析テクニックなどもご紹介します。
- また受講後の実践を想定し、近年多く見かけるようになった共分散構造分析についても各モデルについて、ご紹介します。
・進め方
〇豊富な事例データでそれぞれの分析手法の理解を深める
- データ分析では、分析経験が非常に重要です。スポーツにおいて、座学のみで実際に体験しないと上達しないのと同様、データ分析においても実際に、事例を通して様々なデータ分析を経験することにより身につきます。また、分析の経験があらたな視点の発展にもつながります。
〇実際の分析データを用いて活用
- 難解な講義方式ではなく、興味の持てる具体的な事例データ、確認のための練習問題を活用しながら進めます。
〇受講後の質問にもメール対応致します。(対応期間:受講後3ヶ月間)
【1日目】
1 R基礎
1-1 R、Rstudioのインストール
1-2 Rとは
1-3 Rstudioの使い方
1-4 データの扱い方(DataFrame型)
1-5 Rへのデータの取り込み
1-6 Rからのデータの書き出し
1-7 プログラミングにおける関数の基礎
1-8 スクリプトファイルの作成、保存、使い方
1-9 パッケージの基礎とインストール、使い方
2 統計学基礎
2-1 代表値(平均、中央値、最大値、最小値)
2-2 散布度(分散、標準偏差)
2-3 不偏統計量
2-4 様々な平均(移動平均、幾何平均、調和平均)
2-5 四分位と箱ひげ図
2-6 標準化
2-7 相関(積率相関、順位相関)
2-8 偏相関
2-9 データの種類
2-10 確率分布の基礎
2-11 離散確率分布(ベルヌーイ分布、二項分布、ポアソン分布)
2-12 連続確率分布(正規分布、t分布、カイ二乗分布、F分布)
3 統計的推定
3-1 母集団と標本
3-2 標本調査と標本抽出方法
3-3 区間推定
3-4 1標本の場合(母平均推定、母比率の推定)
3-5 2標本の場合(母平均の差の区間推定、対応のある母平均の差の区間推定)
4 データの可視化
4-1 ヒストグラム、棒グラフ、円グラフ
4-2 折れ線グラフ、バブルチャート
4-3 箱ひげ図
4-4 効果的なグラフの使い方
【2日目】
5 統計的検定の基礎
5-1 検定の誤り(第1種の誤り、第2種の誤り)
5-2 検定の考え方
5-2 効果量の考え方
5-2 検定力の考え方
5-2 サンプルサイズの考え方
5-2 要因計画法の基礎
5-2 データの対応
6 正規性の検定
6-1 コルモゴロフスミノフ検定
6-2 シャピロウィルク検定
7 等分散性の検定
7-1 F検定
7-2 バートレット検定
7-3 ルビーン検定
8 パラメトリック検定
8-1 1標本 t検定
8-2 2標本t検定(対応のない場合)、ウェルチの検定
8-3 対応のある2標本t検定
【3日目】
9 分散分析
9-1 1要因の分散分析(対応なし)
9-2 1要因の分散分析(対応あり)
9-3 2要因の分散分析(対応なし×対応なし)
9-4 2要因の分散分析(対応あり×対応あり)
9-5 2要因の分散分析(対応なし×対応あり)
10 ノンパラメトリック検定
10-1 フィッシャーの正確確率検定
10-2 カイ二乗検定
10-3 マンホイットニーのU検定
10-4 ウィルコクソンの順位和検定
10-5 ウィルコクソンの符号順位和検定
10-6 フリードマン検定
10-7 クラスカルウォリス検定
【4日目】
11 多変量解析
11-1 線形回帰分析(偏回帰係数、決定係数、t検定)
11-1-1 強制投入法、ステップワイズ法
11-1-2 多重共線性
11-1-3 ダミー回帰
11-1-4 交互作用
11-1-5 パス図
11-2 主成分分析(主成分負荷量、寄与率)
11-2-1 主成分得点
11-3 因子分析(因子負荷量、寄与率)
11-3-1 因子抽出方法(主因子法、最尤法)
11-3-2 回転(バリマックス直交、プロマックス斜交)
11-3-3 因子得点
11-4 階層クラスター分析
11-4-1 クラスター化の方法(群平均法、ウォード法、メディアン法、重心法)
11-4-2 距離(ユークリッド、マンハッタン、ミンコフスキー)
11-5 ロジスティック回帰
11-5-1 偏回帰係数、赤池情報量基準(AIC)
11-5-2 オッズ比
12 複数の分析の組み合わせ
12-1 クラスタ―分析のグループごとの回帰分析
12-2 主成分得点を利用した回帰分析
12-3 因子得点を利用した回帰分析
12-4 主成分得点を利用したクラスター分析
12-5 因子得点を利用したクラスター分析
【5日目】
13 共分散構造分析
13-1 適合度指標
CFI、TLI、RMSEA、SRMR、情報量基準(AIC、BIC)
13-2 モデル
13-1-1 逐次モデル (Recursive Model)
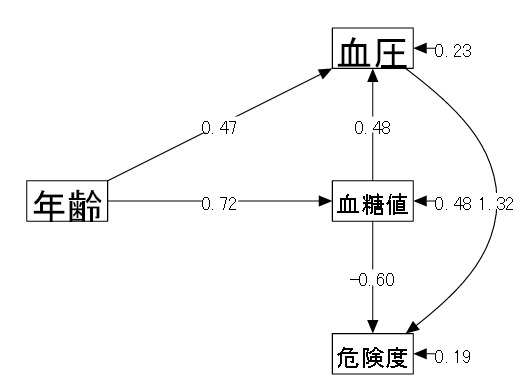
| (1) データ概要 | ある会社の健康診断を受けた男性10名の結果(仮想データ) |
| (2) 変数 | ①年齢 ②血糖値(空腹時) ③血圧(最高値) ④危険度(医者による診断、5段階評価) |
| (3) モデル | 以下のようなモデルを考える。 |
| 「④危険度 ← ②血糖値 + ③血圧」 慢性的な高血糖と高血圧により動脈硬化リスクが高まると考えられる。 | |
| 「②血糖値 ← ①年齢 ③血圧 ← ①年齢」 血糖値、血圧共に加齢による影響を受ける。 | |
| 「③血圧 ← ②血糖値」 高血糖は血液がドロドロなので血圧に影響する。 |
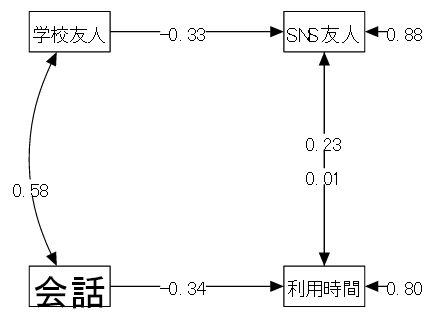
13-1-2 非逐次モデル (non-Recursive Model)
| (1) データ概要 | 高校生100名に対して以下の調査を行った(仮想データ) |
| (2) 変数 | ①利用時間(1日の平均的な利用時間:時間) ②SNS友人(SNSでつながっている友人の数) ③会話(1日の家庭での会話時間の平均:分) ④学校友人(学校で親しくしている友人の数) |
| (3) モデル | 以下のようなモデルを考える。 |
| 「①利用時間 ← ②SNS友人 + ③会話」 スマホ利用時間はネット上での交友関係と家庭での家族との会話の影響を受ける | |
| 「②SNS友人 ← ①利用時間 + ④学校友人」 ネット上の友人は、ネット利用時間と実生活での交友関係の影響を受ける |
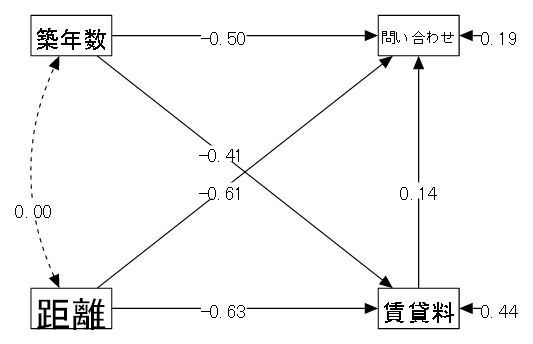
13-2 重回帰分析
| (1) データ概要 | ある駅を最寄り駅とするアパート(間取りはほぼ同じ条件) の各種条件と問い合わせ件数(仮想データ) |
| (2) 変数 | ①賃貸料(月の賃貸料、万円) ②距離(駅からの徒歩による所要時間、分) ③築年数(年) ④問い合わせ(最近1カ月の問い合わせ件数) |
| (3) モデル | 以下のようなモデルを考える。 この例では賃貸料と問い合わせが従属変数となっているため、重回帰分析に該当する。 |
| 「①賃貸料 ← ②距離 + ③築年数」 駅からの距離と築年数によって賃貸料は変わってくる。 | |
| 「④問い合わせ ← ①賃貸料 + ②距離 + ③築年数」 問い合わせの多さは、賃貸料と駅からの距離と築年数 | |
| ②距離と③築年数は関係ないので無相関を仮定する。 |
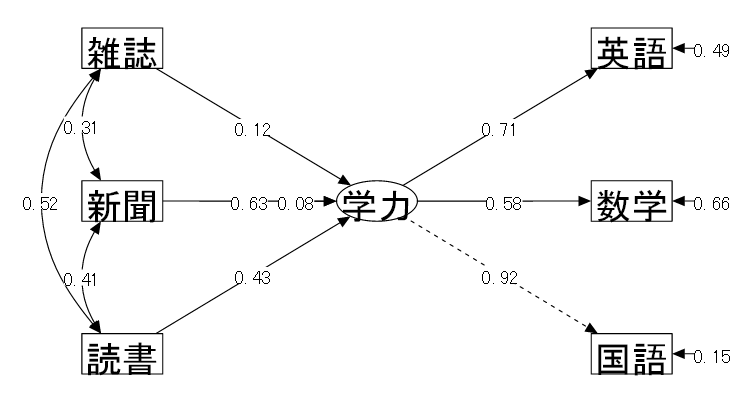
13-3 MIMIC (Multiple Indicator Multiple Cause)
| (1) データ概要 | 中学生25名を対象に以下の調査をした(仮想データ) |
| (2) 変数 | ①読書量(最近1ケ月の間に読んだ本の冊数) ②新聞を読む頻度(1日に新聞を読む平均時間) ③雑誌を読む頻度(1日に雑誌を読む平均時間) ④国語の成績 ⑤数学の成績 ⑥英語の成績 |
| (3) モデル | 3科目の成績から⑦学力という潜在変数を仮定し、3種の活字にふれる頻度が学力に与える影響を確認するようなモデルを立てて検証を行う。 |
| 「⑦学力 = ④国語 + ⑤数学 + ⑥英語」 各科目の成績から潜在変数としての学力が仮定される | |
| 「⑦学力 ← ①読書量 + ②新聞 + ③雑誌」 学力はそれぞれの活字にふれる頻度の影響を受ける |
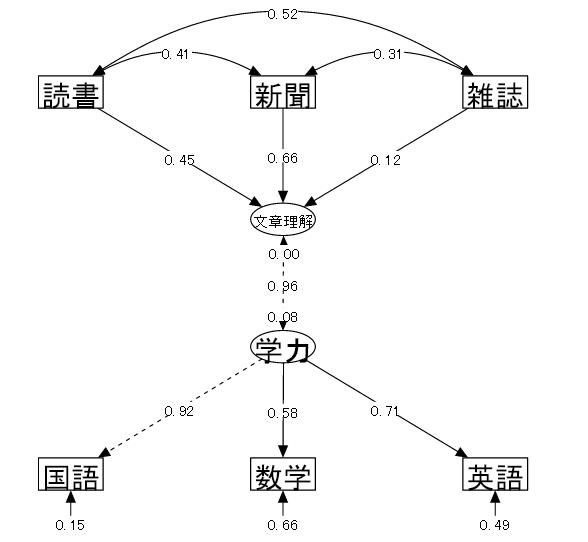
13-4 PLS (Partial Least Squares)
| (1) データ概要 | 中学生25名を対象に以下の調査をした(仮想データ) |
| (2) 変数 | ①読書量(最近1ケ月の間に読んだ本の冊数) ②新聞を読む頻度(1日に新聞を読む平均時間) ③雑誌を読む頻度(1日に雑誌を読む平均時間) ④国語の成績 ⑤数学の成績 ⑥英語の成績 |
| (3) モデル | MIMICの時は潜在変数を「学力」1つとし、その分析結果から仮定された「学力」は文章に関する能力と関連性が強いと想定された。 そこで、もう1つ“学力”と活字にふれる頻度の間に⑧文章理解力という潜在変数を想定し、 3科目の成績から⑦学力という潜在変数を仮定し、3種の活字にふれる頻度が学力に与える影響を確認するようなモデルを立てて検証を行う。 |
| 「⑦学力 = ④国語 + ⑤数学 + ⑥英語」 各科目の成績から潜在変数としての「学力」が仮定される | |
| 「⑧文章理解力 = ⑦学力」 「文章理解力」は「学力」と関係がある | |
| 「⑧文章理解力 ← ①読書量 + ②新聞 + ③雑誌」 「文章理解力」はそれぞれの活字にふれる頻度の影響を受ける | |
| ⑧文章理解力の分散を0に指定する。 | |
| 「文章理解力」は矢印を受ける従属変数ではあるが、もう1つの潜在変数である「学力」とは異なる変数であり、モデル上では、3つの活字にふれる頻度の変数のみから表現されるものとして扱う。 |
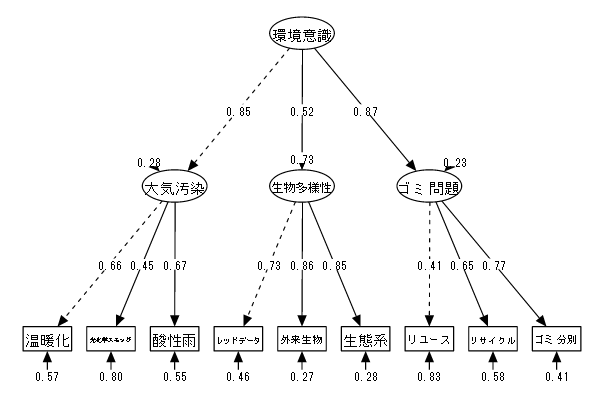
13-5 2次因子分析
| (1) データ概要 | 100名を対象に以下の項目についての知識度を測定、7段階で評価した(仮想データ) |
| (2) 変数 | ①温暖化 ②光化学スモッグ ③酸性雨 ④レッドデータ ⑤特定外来生物 ⑥生態系 ⑦リユース ⑧リサイクル ⑨ゴミ分別 |
| (3) モデル | 大気汚染、生物多様性、ゴミの3つの問題に対する意識の高さを潜在変数として仮定し、 この3潜在変数から更に2次的な潜在変数として環境問題への意識を仮定する。 |
| 「⑩大気汚染 = ①温暖化 + ②光化学スモッグ + ③酸性雨」 「⑪生物多様性 = ④レッドデータ + ⑤特定外来生物 + ⑥生態系」 「⑫ゴミ問題 = ⑦リユース + ⑧リサイクル + ⑨ゴミ分別」 「⑬環境意識 = ⑩大気汚染 + ⑪生物多様性 + ⑫ゴミ問題」 |